∫p / pP [n]  [+,/ ]  w/ sen s + cós c / [p] ∞ = siG [a], ∫ / [ p / pP  [+,/ ]  w/ sen s + cós c / [p] ∞[n] ] = ∫siG [b] [n]

        

  ∫ log x / x [n]k cc [p/pP]∞ , k cx [p/pP = siG [a], ∫ / [log x / x [n]k cc [p/pP]∞ , k cx [p/pP =  ∫ siG [b],] [n]

 

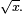
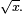 p / pP [+,/ ]  w/ sen s + cós c / [p] ∞ [n] = siG [a],  ∫ /  [ p / pP  [+,/ ]  w/ sen s + cós c / [p] ∞ [n] ] =siG [b] [n]

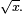 *. log x / x [n][ lt [w a q[nd, Fo]],], LG [u a k [nd, Fo]], AL [h a g[nd, Fo]],] [rx] ] [n], [ a, w, p, p/pP]. [ acq,]  = siG [a], /  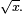* [log x / x [n][ lt [w a q[nd, Fo]],], LG [u a k [nd, Fo]], AL [h a g[nd, Fo]],] [rx] ] [n], [ a, w, p, p/pP]. [ acq,]  = siG [b],] [n]

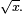 *. log x / x [n]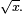R / pi = siG [a], /  * [log x / x [n]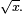R / pi = siG [b],]  p / pP [n] R / pi= siG [c], [n]

outro caminho para funções dentro de funções.